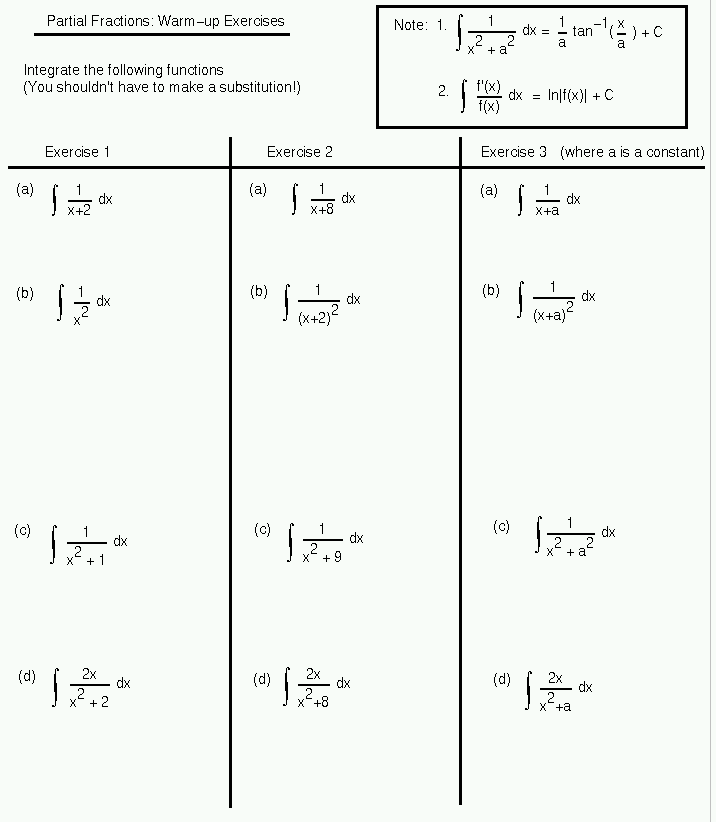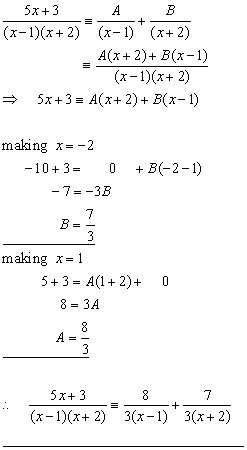Integration By Partial Fractions Pdf

We will focus on rational functions p x q x such that the degree of the numerator p x is strictly less than the degree of q x.

Integration by partial fractions pdf. By parts by partial fractions integration by parts is used to integrate a product such as the product of an algebraic and a transcendental function. Fractions in which the denominator has a quadratic term 6 6. Expressing a fraction as the sum of its partial fractions 3 4. These pdf slides are con gured for viewing on a computer screen.

Quotients of linears so we can integrate z 8x 14 3x 9 dx by writing it as z 8 3 3x 9 38 3x 9 dx and separating to get z 8 3 3x. That is we want to compute z p x q x dx where p q are polynomials. Revision of adding and subtracting fractions 2 3. Xexdx xxsin d xxln dx etc.

If the integrand the expression after the integral sign is in the form of an algebraic fraction and the integral cannot be evaluated by simple methods the fraction needs to be expressed in partial fractions before integration takes place. Integration using partial fractions this technique is needed for integrands which are rational functions that is they are the quotient of two polynomials. Factor and decompose into partial fractions getting after getting a common denominator adding fractions and equating numerators it follows that. Click here to return to the list of problems.

Method of partial fractions when f x g x is proper degf x degg x 1. Z x2 5x 7 x2 25x 6 dx z 1 1 x 5x 6 dx z dx z. Dd uv uv uv v u dx dx dx udv. A1 x r a2 x r 2a3 x r 3a.

Fractions where the denominator has a repeated factor 5 5. Solutions to integration by partial fractions solution 1. First reduce1 the integrand to the form s x r x q x where r q. Joe foster integration by partial fractions summary.

The steps needed to decompose an algebraic fraction into its partial fractions results from a consideration of the reverse process addition or. From the product rule for differentiation for two functions u and v. Integration by partial fractions we now turn to the problem of integrating rational functions i e functions of the form p x q x where p x and q x are polynomials. We can sometimes use long division in order to rewrite such an integrand into a sum of functions whose antiderivatives we can easily find.

Let x r be a linear factor of g x suppose that x r m is the highest power of x r that divides g x then to this factor assign the sum of the m partial fractions. Let recall that. Express an algebraic fraction as the sum of its partial fractions contents 1. Viewing them on hand held devices may be di cult as they require a slideshow.

Integration by partial fractions step 1 if you are integrating a rational function p x q x where degree of p x is greater than degree of q x divide the denominator into the numerator then proceed to the step 2 and then 3a or 3b or 3c or 3d followed by step 4 and step 5.